程序猿养成之路：经典Top K 问题

2021-03-08

面试经典问题——Top K问题

问题描述

从arr[1, n]这n个数中，找出最大的k个数，这就是经典的TopK问题。

解法

一、排序

最容易想到的方法，通过如快排等效率较高的排序算法，可以在平均 O（nlogn）的时间复杂度找到结果。这种方式在数据量不大的时候简单可行，但固然不是最优的方法。

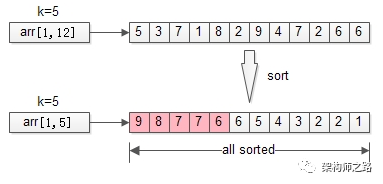
伪代码：

1 2	sort(arr, 1, n); return arr[1, k];

时间复杂度：$O(nlg(n))$

分析：明明只需要TopK，却将全局都排序了，这也是这个方法复杂度非常高的原因。那能不能不全局排序，而只局部排序呢？这就引出了第二个优化方法。

二、局部排序

不再全局排序，只对最大的k个排序。

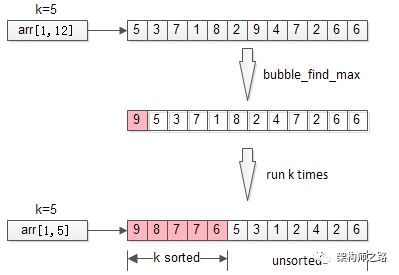
伪代码：

for(i=1 to k){
	bubble_find_max(arr,i);
}
return arr[1, k];

时间复杂度：O(n*k)

分析：冒泡，将全局排序优化为了局部排序，非TopK的元素是不需要排序的，节省了计算资源。不少朋友会想到，需求是TopK，是不是这最大的k个元素也不需要排序呢？这就引出了第三个优化方法。

三、堆

最经典的解法还是利用堆，因为利用堆可以使用很小的内存处理Top K问题。当有海量数据的时候，内存不可能同时放得下这么数据，上述两种排序的方法不可行。

维护一个大小为 K 的小顶堆，依次将数据放入堆中，当堆的大小满了的时候，只需要将堆顶元素与下一个数比较：如果大于堆顶元素，则将当前的堆顶元素抛弃，并将该元素插入堆中。遍历完全部数据，Top K 的元素也自然都在堆里面了。当然，如果是求前 K 个最小的数，只需要改为大顶堆即可

将数据插入堆

95 大于 20，进行替换

95 下沉，维持小顶堆

伪代码：

heap[k] = make_heap(arr[1, k]);
	for(i=k+1 to n){
		adjust_heap(heep[k],arr[i]);
	}
return heap[k];

时间复杂度：O(n*lg(k))

分析： 对于海量数据，我们不需要一次性将全部数据取出来，可以一次只取一部分，因为我们只需要将数据一个个拿来与堆顶比较。

另外还有一个优势就是对于动态数组，我们可以一直都维护一个 K 大小的小顶堆，当有数据被添加到集合中时，我们就直接拿它与堆顶的元素对比。这样，无论任何时候需要查询当前的前 K 大数据，我们都可以里立刻返回给他。

整个操作中，遍历数组需要 O(n) 的时间复杂度，一次堆化操作需要 O(logK)，加起来就是 O(nlogK) 的复杂度，换个角度来看，如果 K 远小于 n 的话， O(nlogK) 其实就接近于 O(n) 了，甚至会更快，因此也是十分高效的。

四、随机选择

随机选择算在是《算法导论》中一个经典的算法，其时间复杂度为O(n)，是一个线性复杂度的方法。快排的 partition 划分思想可以用于计算某个位置的数值等问题，例如用来计算中位数；显然，也适用于计算 TopK 问题。

伪代码

int RS(arr, low, high, k){
	if(low== high) return arr[low];
	i= partition(arr, low, high);
	temp= i-low; //数组前半部分元素个数
	if(temp>=k)
		return RS(arr, low, i-1, k); //求前半部分第k大
	else
		return RS(arr, i+1, high, k-i); //求后半部分第k-i大
}

时间复杂度： 这是一个典型的减治算法，递归内的两个分支，最终只会执行一个，它的时间复杂度是O(n)。

分析： 每次经过划分，如果中间值等于 K ，那么其左边的数就是 Top K 的数据；
当然，如果不等于，只要递归处理左边或者右边的数即可

该方法的时间复杂度是 O(n) ，简单分析就是第一次划分时遍历数组需要花费 n，而往后每一次都折半（当然不是准确地折半），粗略地计算就是 n + n/2 + n/4 +… < 2n，因此显然时间复杂度是 O(n)。

其他Top K系列问题

海量数据中查找频率最高的K个数

问题描述

有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M，要求返回频数最高的100个词

思路

采用分治法的思想，利用hash映射把大文件分成小文件（这个例子里可以采取hash(x)%5000，把数据存储到5000个小文件中，每个文件大概是200k左右）；
用hashmap记录每个词出现的频率（桶的思想）；
转化为上文Top K问题——查找频率最大的K个数，采用最小堆的方法；
归并每个子文件，再进行Top K问题的求解。

海量数据查找中位数

问题描述

只有2G内存的pc机，在一个存有10G个整数的文件，从中找到中位数，写一个算法。

思路

借鉴基数排序思想

可以用位来判断计数，从最高位到最低位，为了方便表述我们假设为无符号整数，即0x00000000~0xFFFFFFFF依次递增，那么可以遍历所有数据，并记录最高位为0和1的个数（最高位为0的肯定是小于最高位为1的）记为N0、N1
那么根据N0和N1的大小就可以知道中位数的最高位是0还是1
假设N0>N1，那么再计算N00和N01，
如果N00>(N01+N1)，则说明中位数的最高两位是00
再计算N000和N001.。。。依次计算就能找到中位数
借鉴桶排序的思想

一个整数假设是32位无符号数
第一次扫描把数字2^16个区间，记录每个区间的整数数目
找出中位数具体所在区间
第二次扫描则可找出具体中位数数值